17. Máximos e Mínimos
Uma das principais utilizações do cálculo está em problemas de otimização, nos quais temos uma quantidade e desejamos encontrar seu valor máximo ou mínimo. Isso é frequentemente de extrema importância em questões de engenharia, onde é altamente desejável saber quais condições tornarão o custo de operação mínimo ou a eficiência máxima.
Historicamente, um dos principais problemas que preocupava os cientistas era o de encontrar os maiores ou menores valores de quantidades variáveis. A maior distância que poderia ser obtida variando o ângulo de elevação de um canhão e a maior e menor distância de um planeta ao sol são exemplos de problemas reais daquela época. Por que esses problemas teriam levado ao pensamento sobre o cálculo, ou seja, sobre taxas de variação instantânea?
Fisicamente, era claro para os cientistas que uma taxa de mudança estava envolvida. Considere uma bola lançada diretamente para cima no ar. À medida que ela sobe, sua velocidade diminui; quando atinge o ponto mais alto, a altura máxima, sua velocidade é 0, caso contrário, ela continuaria a subir. Em outras palavras, a velocidade é 0 na altura máxima. Mas a velocidade é a taxa de variação instantânea da altura em relação ao tempo. Portanto, a taxa de variação instantânea ou a derivada está envolvida. Esperamos então que também esteja envolvida em outros problemas de máximos e mínimos.
Antes, é importante ter em mente o que significa um máximo ou um mínimo. Dizemos que \(x_0\) é um ponto de máximo de \(f\) se \(f(x_0)\geq f(x)\) para qualquer \(x\) no domínio da função \(f.\) Agora se esta propriedade ocorre apenas para valores próximos a \(x_0\), isto é, existem \(a\) e \(b\) tais que \(a<x_0<b\) e \(f(x)\geq f(x_0)\) para qualquer \(x\) que satisfaz \(a<x<b,\) então dizemos que \(x_0\) é um ponto de máximo local de \(f.\) O valor de \(f\) em \(x_0,\) \(f(x_0)\), é chamado de valor máximo ou valor máximo local.
Podemos definir de forma similar o que é um ponto mínimo ou mínimo local de \(f\) e o valor mínimo ou valor mínimo local de \(f.\)
Na animação abaixo, mova o ponto para ver como a derivada da função está mudando. Note que nos pontos de máximo e mínimo, a derivida da função é igual a zero.
O cálculo tem algo simples e marcante a dizer sobre os pontos de máximo e mínimo (locais): em tal ponto, a reta tangente ao gráfico é horizontal; em outras palavras, \(f'(x_0) = 0.\)
Essa afirmação parece ser muito fácil de acreditar - certamente parece verdadeira em figuras. No entanto, não se pode fundamentar a aceitação de um fato em algumas imagens. E existem uma infinidade de imagens diferentes que se poderia desenhar para ilustrar o mesmo ponto. Como pode ficar realmente claro que a reta tangente será horizontal em todos os casos?
Note que se \(x_0\) é um ponto de máximo local de \(f\), então existe um \(\delta>0\) suficientemente pequeno tal que
\(\displaystyle f(x_0)\geq f(x_0+h),\text{ para todo }|h|<\delta.\)
Logo, se \(h>0,\) temos
\(\displaystyle f(x_0+h)-f(x_0)\leq 0\Rightarrow \frac{f(x_0+h)-f(x_0)}{h}\leq 0.\)
Similarmente, se \(h<0,) temos
\(\displaystyle f(x_0+h)-f(x_0)\leq 0\Rightarrow \frac{f(x_0+h)-f(x_0)}{h}\geq 0.\)
As equações acima implicam então
\(\displaystyle 0\leq f'(x_0)=\lim_{h\to0}\frac{f(x_0+h)-f(x_0)}{h}\leq 0\Rightarrow f'(x_0)=0.\)
A prova quando \(f\) tem um mínimo local em \(x_0\) é basicamente a mesma, exceto que todas as desigualdades são invertidas.
Exemplo 1. Suponha que você é um agricultor e deseja criar um campo retangular ao lado de um rio (veja a animação abaixo). Suponha, também, que você tenha uma quantidade fixa de cercas - digamos 4 km - para os outros três lados. Como você deve organizar as coisas para que a área \(A\) do campo seja a maior possível? Deveria, por exemplo, escolher o retângulo de forma que seja um quadrado? Devo confessar que nunca conheci um agricultor que quisesse fazer algo do tipo, mas este problema simples ilustra bem um aspecto particular do cálculo em ação.
Para entender esse problema, vamos usar \(x\) para representar a largura do campo, de modo que o lado paralelo ao rio deve ter um comprimento de \(4 − 2x.\) A área do campo, portanto, será \(x\cdot(4 − 2x),\) então
\(\displaystyle A(x)=4x-2x^2,\)
e nosso problema é escolher \(x\) de modo que \(A\) seja um máxima. E o passo chave é diferenciar em relação a \(x,\) o que nos dá
\(\displaystyle \frac{dA}{dx}=4-4x.\)
Agora, claramente, \(\displaystyle \frac{dA}{dx}=0\) se \(x=1.\)
É importante perceber que uma derivada igual a zero em \(x_0\) não implica um extremo em \(x_0.\) Por exemplo, vamos considerar \(f(x) =x^3.\) O gráfico de \(f\) é mostrado abaixo. Aqui, \(f'(x) = 3x^2,\) então \(f'(0) = 0.\) No entanto, essa função está aumentando em todos os intervalos que contêm \(0,\) portanto, não há extremo em \(0.\) Este exemplo mostra que uma derivada igual a zero em \(x_0\) não é suficiente para um extremo em \(x_0.\)
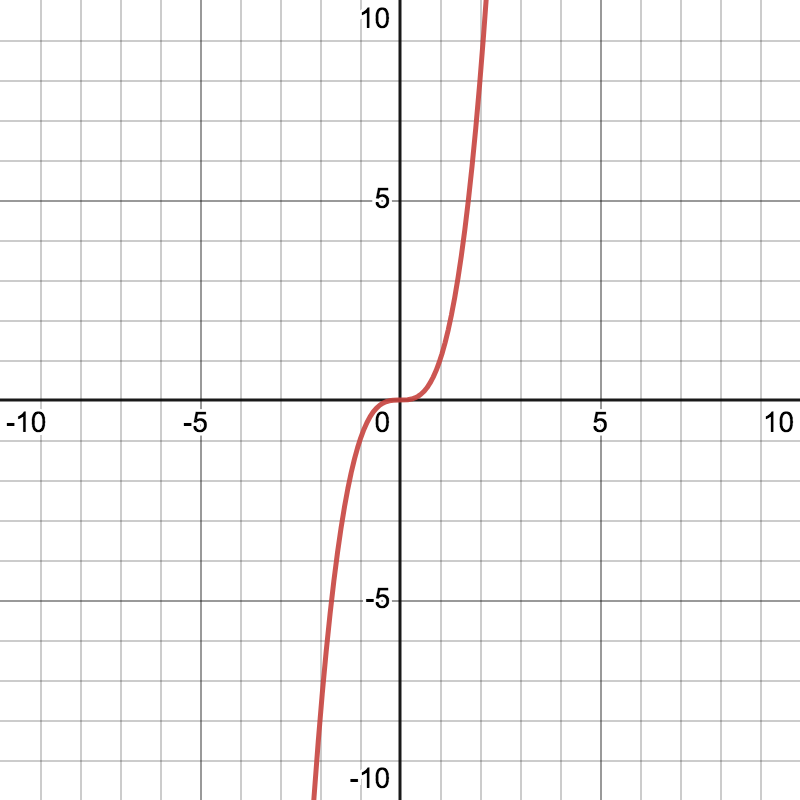
Portanto, se \(f\) tiver um máximo ou mínimo (local) em \(x_0,\) então \(f'(x_0)\) deve ser \(0,\) mas apenas porque \(f'(x_0) = 0,\) não podemos concluir que \(x_0\) é um ponto de máximo ou mínimo local.
Felizmente, essa complicação não diminui o valor da propriedade da derivada, quando existir, ser zero em ponto de máximo ou mínimo local na resolução desses problemas de "max-min" - ainda é verdade que podemos encontrar todas as possibilidades para um máximo ou mínimo encontrando todos os \(x_0\) para os quais \(f'(x_0) = 0;\) o único problema é que todos esses \(x_0\) são apenas candidatos, que então precisam ser examinados com mais cuidado para determinar sua adequação.
Exemplo 2. Onde você deve entrar em uma rodovia expressa para minimizar o tempo de viagem entre dois pontos, \(A\) e \(B), se a velocidade na rodovia expressa é de 100 km/h e a velocidade de condução comum (dentro da cidade) é de 50 km/h?
A maioria dos modelos é simplificada para focar na ideia principal. Vamos permitir que a rodovia expressa seja acessada em qualquer ponto \(x\) (veja a animação abaixo). Em vez de duas entradas (um problema discreto), temos uma escolha contínua (um problema de cálculo). A viagem tem duas partes, a velocidades de 50 km/h e 100 km/h:
Uma distância \(\sqrt{a^2+x^2}\) até a rodovia expressa, em \(\displaystyle \frac{\sqrt{a^2+x^2}}{50}\) horas;
Uma distância \(b - x\) na rodovia expressa, em \(\displaystyle \frac{b - x}{100}\) horas.
O problema então é minimizar o tempo total da viagem, que é \(\displaystyle f(x)=frac{\sqrt{a^2+x^2}}{50}+\frac{b - x}{100}.\)
Temos a função \(f(x)\). Agora entra o cálculo. O primeiro termo utiliza a regra da potência: A derivada de \(\displaystyle u^{1/2}\) é \(\displaystyle\frac{1}{2}u^{-1/2}\frac{du}{dx}.\) Aqui, \(\displaystyle u=a^2+ x^2,\) e \(\displaystyle\frac{du}{dx} = 2x:\)
\(\displaystyle f'(x)=\frac{1}{50}\cdot\frac{1}{2}(a^2+x^2)^{-1/2}\cdot 2x-\frac{1}{100}.\)
Logo \(f'(x)=0\) é o mesmo que
\(\displaystyle \frac{2x}{100}(a^2+x^2)^{-1/2}=\frac{1}{100}\Rightarrow 2x=(a^2+x^2)^{1/2}\Rightarrow 4x^2=a^2+x^2\Rightarrow 3x^2=a^2.\)
Como \(x>0,\) temos \(\displaystyle x=\frac{a}{\sqrt{3}}.\)
Você pode notar algo surpreendente. O ponto estacionário \(\displaystyle x = \frac{a}{\sqrt{3}}\) não depende de \(b.\) O tempo total inclui o valor constante \(b/100,\) que desapareceu na derivada \(\displaystyle \frac{df}{dx}.\) De alguma forma, \(b\) deve entrar na resposta, e isso é um aviso para proceder com cuidado. O mínimo pode ocorrer em um ponto irregular ou em um ponto final. Esses são os outros pontos críticos de \(f,\) e nosso desenho pode não ser realista. Certamente esperamos que \(x\leq b.\)
Calculando o valor de \(f\) em \(\displaystyle x\frac{a}{\sqrt{3}},\) temos
\(\displaystyle f\left(\frac{a}{\sqrt{3}}\right)=\frac{1}{50}\cdot\sqrt{a^2+\frac{a^2}{3}}+\frac{1}{100}\cdot\left(b-\frac{a}{\sqrt{3}}\right)=\frac{1}{50}\sqrt{\frac{4a^2}{3}}+\frac{1}{100}\left(b-\frac{a}{\sqrt{3}}\right)=\frac{b}{100}+\frac{3a}{100\sqrt{3}}=\frac{1}{100}(b+\sqrt{3}a).\)
Agora, em \(x=0\), temos
\(\displaystyle f(0)=\frac{a}{50}+\frac{b}{100}=\frac{1}{100}(b+2a).\)
Finalmente, em \(x=b,\) temos
\(\displaystyle f(b)=\frac{\sqrt{a^2+b^2}}{50}.\)
Claramente, \(\displaystyle f(0)\geq f\left(\frac{a}{\sqrt{3}}\right).\) Para comparar \(\displaystyle f\left(\frac{a}{\sqrt{3}}\right)\) e \(f(b)\) é necessário ver que se \(\displaystyle \frac{a}{\sqrt{3}}\leq b,\) então \(\displaystyle f\left(\frac{a}{\sqrt{3}}\right)\leq f(b),\) mas se \(\displaystyle \frac{a}{\sqrt{3}}> b,\) então \(\displaystyle f\left(\frac{a}{\sqrt{3}}\right)> f(b).\)